数学笔记
因式分解
简介
因式分解,简单来说就是把一个多项式(如x^2+2x+1)分解成两个或多个的因式的过程。在这之后,我们会得到几个比较简单的多项式。
例如:
如果你把右边的(x+y)(x-y)拿来相乘,你会得到:
由此就可以证明,(x+y)(x-y)是x^2-y^2的因式。
因式分解常用的公式
因式分解的种类
1)
抽取法
2)
十字交乘法(Cross Method)
3)
分组法
4)
假设法
5)
添项法
6)
拆项法
7)
双十字交乘法
这七个种类的难度由浅到深。一般如果是要通过SPM,学会前三个大致就ok了,当然,如果七种都能掌握,无论你是初中高中,或Form几都可以比较快速地解决因式分解相关的问题。
(1) 抽取法
这种方法是最简单的,如果看到一个多项式里有公因子,就直接提取一个公因子再说,这样整个问题就可以被简化了。
例题:
(2) 十字交乘法(Cross Method)
简单的十字交乘法就是上面提到的公式(x+a)(x+b)=
x^2+(a+b)x+ab的运用。
例题:
找出x^2-2x-15的因式。
(3) 分组法
这个方法是通过把公式重组,重新分组后再抽取它们的公因子,从而达成因式分解的目的。但是分组法有的时候没那么容易看出来,可能需要一点感觉。
例题:
(4) 假设法/求根法
令多项式等于0,然后代入数字,看等式是否成立,如果成立就代表这是其中一个因式。
例题:
因式分解x^3-2x^2+5x-4。
f(x)= x^3-2x^2+5x-4
f(2)=2^3-2*2^2+5*2-4=
8-8+10-4= 6
(x-2)并不是这多项式的因式。
f(1)=
1^3-2*1^2+5*1-4= 0
由此可知x^3-2x^2+5x-4的其中一个因式为(x-1)。通过长除法,就可以得出x^3-2x^2+5x-4= (x-1)(x^2-x-4)
(5) 添项法
在方程式里增加两个完全相反的项。一般通过添项来构成完全平方公式或者立方差或立方和公式;当然,有时则需根据系数配成十字相乘法的形式。
例题:
(6) 拆项法
把方程式里的一个项拆开来,将需要拆掉的项按照其余项的系数绝对值拆分。和添项法一样,都是为了要凑成完全平方工时或立方差公式或立方和公式。
例题:
(7) 双十字交乘法
比十字相乘法更high level的就是双十字交乘法。双十字相乘法主要应用在二元二次方程式。例如ax^2+by^2+cxy+dx+ey+f,当中abcdef都是常数,只有x和y是未知数。
用双十字交乘法有三个步骤:
一、分解ax^2+by^2+cxy,以得到a1、a2、b1、b2的值
二、把常数f拆成f1和f2,a1f2+a2f1=d的值,b1f2+b2f1=e的值
三、最后就可以得到ax^2+by^2+cxy+dx+ey+f= (a1x+b1y+f1)(a2x+b2y+f2)
看上去有点复杂?没关系,可以看例题:
例题:
练习题和答案请看这里

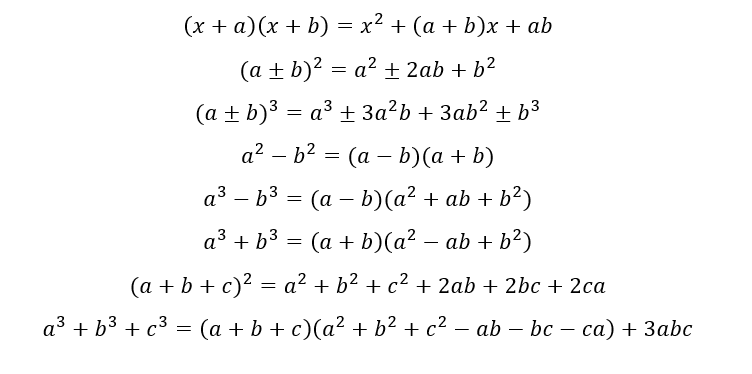



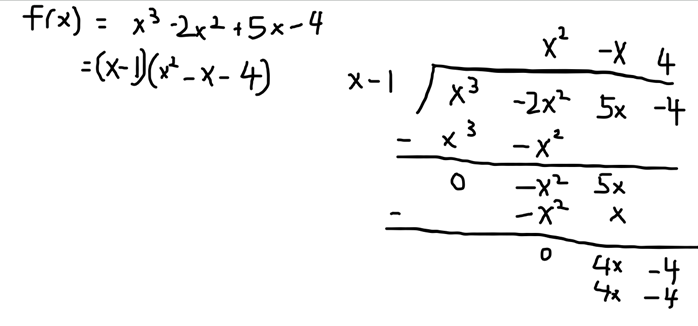





Comments
Post a Comment